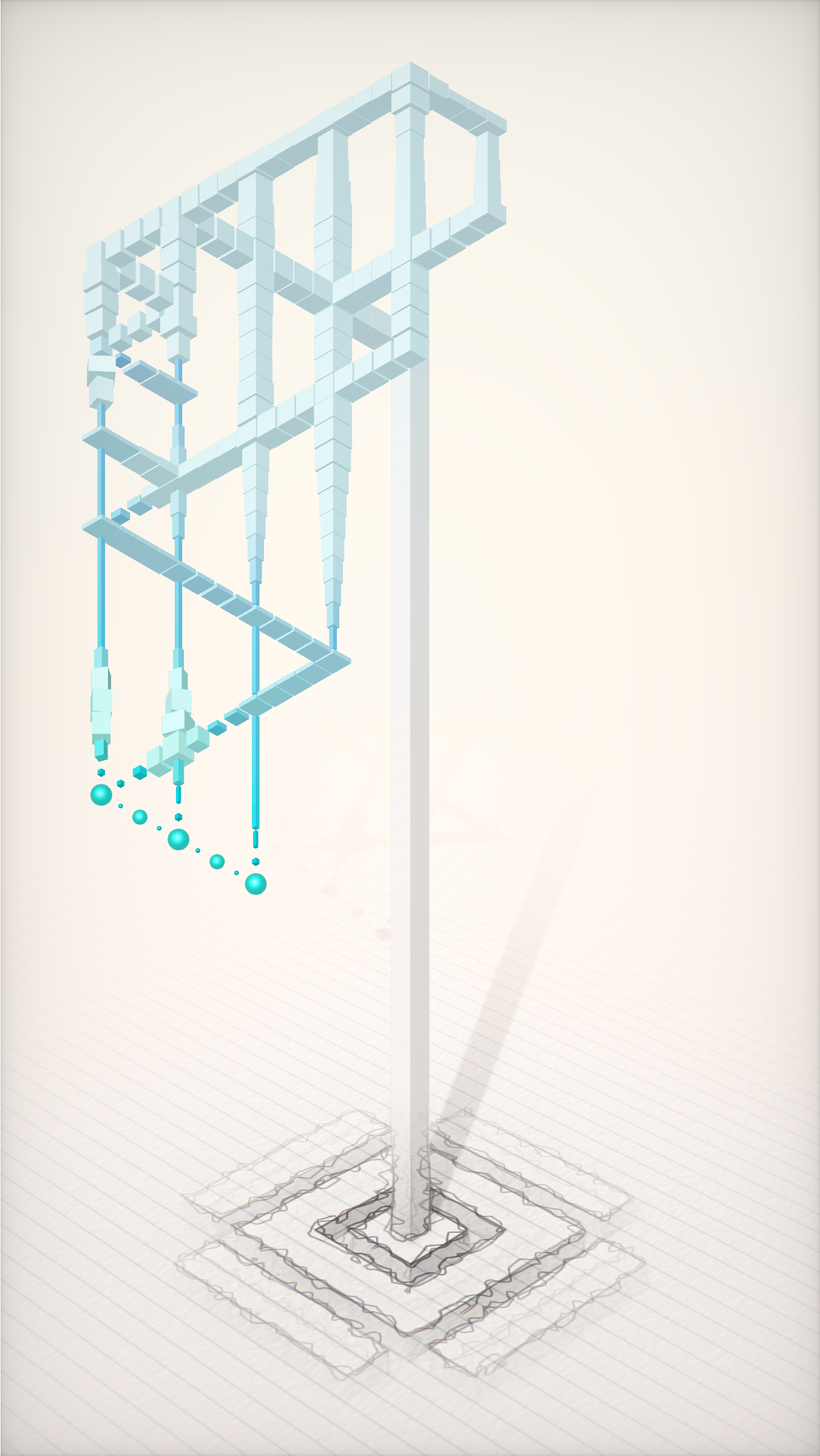
Escherly Seeds #4

This is my algorithmic love letter to a forefather of mathematical art: M. C. Escher. To commemorate 125 years since his birth, my goal was to honor Escher’s enduring influence by reworking his iconic motifs into a medium that embraces mathematics as much as he did.

I gave it the name Escherly Seeds because its meaning is three-fold:

• Metaphorical. This work can be seen as representing the seeds that Escher planted in the minds of the artistic community, and I make several references to his work. Concave and Convex (1955) and Waterfall (1961) were the main inspirations for up to three distinct optical illusions hidden within this algorithm. Expect Escher’s love of polyhedra – a few of which can be seen in Stars (1948) – to make appearances too!

• Arboreal. This metaphor is illustrated as a tree with surrealist botanical components. It starts out, drawn on paper, as a root network from which a stem sprouts, branching into a fully developed crown with leaves, flowers, and/or fruit. Flowers are depicted as enlarged polyhedra with special properties, and fruit are cyclical structures inspired by the iconic Penrose triangle. Fruit can also, on occasion, be ripe with its own seeds, thus completing its life cycle. The pencil-to-3D effect is a reference to Reptiles (1943) and Drawing Hands (1948), except I take the metamorphosis to the present – becoming fully chromatic, dynamic, and interactive. The seed is planted in Escher’s world, and blossoms into ours.

• Cryptographic. Generative art is, in a way, the craft of making pseudo-random art generators. Each output is the result of a cascade of calculations caused by one unique numerical seed, and in this case, it just happens to be an “Escherly” seed! For those curious about the details, I tried to avoid excessively obfuscating the code.

The viewer is encouraged to play with the artwork! In an effort to make the tree feel alive, I used an equation called the Kuramoto model which, most notably, mimics the flashing patterns observed in species of synchronous fireflies. Each cube is animated by an internal “clock” which is weakly coupled to its nearest neighbors. Interacting with these clocks will cause them to align, giving you the ability to synchronize or desynchronize certain areas of the tree.

The collection size is set to 327 because March 27 is the date Escher passed away.

Thank you to all who helped me along the way, no matter the weight of your contribution.

Special thanks: Jiahui Cai, Vincent Cohen, Daniel Bothner